MatheAss 9.0 - Álgebra Lineal
Sistemas de ecuaciones lineales
El programa determina el vector solución a partir de un sistema de ecuaciones lineales con n ecuaciones y n incógnitas.
Ejemplo: Buscar una parÁbola a través de los puntos P(1|3), Q(2|1) y R(4|9) conduce al sistema de ecuaciones
1·x1 + 1·x2 + 1·x3 = 3
4·x1 + 2·x2 + 1·x3 = 1
16·x1 + 4·x2 + 1·x3 = 9
L = (2; -8; 9)
Por tanto, la parÁbola se describe mediante y = 2x 2 - 8x + 9.
Ejemplo con bidimensional solución:
0·x1 + 0·x2 + 2·x3 - 1·x4 = 1
1·x1 + 1·x2 + 1·x3 + 1·x4 = 4
2·x1 + 2·x2 - 4·x3 + 5·x4 = 5
1·x1 + 1·x2 - 7·x3 + 5·x4 = 0
L = { ( 3,5-s-1,5t; s; 0,5+0,5t; t ) | s,t ∈ R }
Optimización lineal
( desde febrero 2022 )
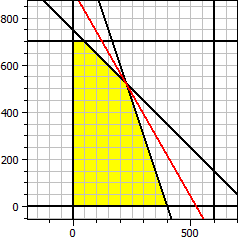
El programa determina la solución óptima para una función objetivo de dos variables con restricciones.
Función objetivo: ƒ(x,y) = 140·x + 80·y → Maximum Restricciones: x ≥ 0 y ≥ 0 x ≤ 600 y ≤ 700 x + y ≤ 750 3·x + y ≤ 1200 Máximo: x = 225 y = 525 ƒ(x,y) = 73500
Combinación lineal
La combinación lineal de un vector a cabo de tres vectores linealmente independientes se determina. La rutina también es adecuada para verificar la independencia lineal de tres vectores en el espacio, es decir, si se encuentran en un plano.
⎧ 1 ⎫ ⎧ 1 ⎫ ⎧ 1 ⎫ ⎧ 2 ⎫
a·⎪ 0 ⎪ + b·⎪ 1 ⎪ + c·⎪ 1 ⎪ = ⎪ 3 ⎪
⎩ 0 ⎭ ⎩ 0 ⎭ ⎩ 1 ⎭ ⎩ 4 ⎭
Solución:
a = -1 b = -1 c = 4
Producto escalar
Dados dos vectores el producto escalar, la longitud de los vectores y el ángulo se calculan.
-> ⎧ 1 ⎫ -> ⎧ 5 ⎫
a = ⎪ 3 ⎪ b = ⎪ 0 ⎪
⎩ 1 ⎭ ⎩ 3 ⎭
Producto escalar del vectores = 8
La longitud del primer vector = √11 = 3.32
La longitud del segundo vector = √34 = 5.83
Ángulo incluido α = 65.56°
Producto vectorial
Dados dos vectores el producto y la magnitud del vectores se calculan. El producto vectorial es perpendicular al paralelogramo generado por ti, y su valor es igual al Área del paralelogramo.
-> ⎧ 1 ⎫ -> ⎧ 7 ⎫
a = ⎪ 2 ⎪ b = ⎪ 1 ⎪
⎩ 3 ⎭ ⎩ 4 ⎭
-> -> ⎧ 5 ⎫ -> ->
a x b = ⎪ 17 ⎪ |a x b|= √483 = 21,977261
⎩-13 ⎭
Producto mixto
Dados tres vectores el producto mixto se calcula.Su valor indica el volumen del paralelepípedo desplazado (espÁtula) que abarcan los tres vectores.
-> ⎧ 2 ⎫ -> ⎧ 2 ⎫ -> ⎧ 3 ⎫
a = ⎪ 3 ⎪ b = ⎪-1 ⎪ c = ⎪ 9 ⎪
⎩ 5 ⎭ ⎩ 7 ⎭ ⎩ 2 ⎭
-> -> ->
( a x b ) · c = 26
Matriz de Inversión
El programa calcula el determinante, el rango y la matriz inversa para una matriz cuadrada de orden n.
Matriz : ¯¯¯¯¯¯¯¯ ⎧ 1 0 2 ⎫ ⎪ 0 1 0 ⎪ ⎩ 3 0 1 ⎭ Matriz inversa : ¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯ ⎧-0,2 0 0,4 ⎫ ⎪ 0 1 0 ⎪ ⎩ 0,6 0 -0,2 ⎭ Orden = 3, rango = 3, determinante = -5
Matriz pseudo inversa
Matriz A ¯¯¯¯¯¯¯¯ ⎧ 1 1 1 1 ⎫ ⎩ 5 7 7 9 ⎭ A · AT ¯¯¯¯¯¯ ⎧ 4 28 ⎫ ⎩ 28 204 ⎭ ( A · AT )-1 ¯¯¯¯¯¯¯¯¯¯¯¯ ⎧ 6,375 -0,875 ⎫ ⎩-0,875 0,125 ⎭ Inversa derecha: AT·( A·AT )-1 ¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯ ⎧ 2 -0,25 ⎫ ⎪ 0,25 0 ⎪ ⎪ 0,25 0 ⎪ ⎩ -1,5 0,25 ⎭
Si las filas de la matriz A son linealmente independientes, obtenemos el pseudo inverso con la fórmula:
A+ = AT · (A · AT )-1
Esta es una inversa derecha de A , lo que significa:
Si las columnas de la matriz A son linealmente independientes, obtenemos el pseudo inverso con la fórmula:
A+ = (AT · A)-1 · AT
Esta es una inversa izquierda de A , lo que significa:
Multiplicación de matrices
Dadas dos matrices A1 y A2 el producto se calcula.
1. Matriz : ¯¯¯¯¯¯¯¯¯¯ ⎧ 1 0 2 ⎫ ⎩ 0 1 0 ⎭ 2. Matriz : ¯¯¯¯¯¯¯¯¯¯ ⎧-0,2 0 0,4 1 ⎫ ⎪ 0 1 0 1 ⎪ ⎩ 0,6 0 -0,2 1 ⎭ Producto de matrices: ¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯ ⎧ 1 0 0 3 ⎫ ⎩ 0 1 0 1 ⎭
