MatheAss 10.0 − Geometría 2D
Triángulos rectángulos
Habida cuenta de dos de los elementos de un triángulo rectángulo, los otros se calculan.
Dado
¯¯¯¯¯
Cateto a = 3
Cateto b = 5
Resultados
¯¯¯¯¯¯¯¯¯
Hipotenusa c = 5,8309519
Angulo α = 30,963757°
Angulo β = 59,036243°
Segmento hipot. p = 1,5434873
Segmento hipot. q = 4,2874646
Altura h = 2,5724788
Área A = 7,5
Triángulos por tres elementos
Teniendo en cuenta tres elementos de cualquier triángulo, el programa calcula los lados, alturas, medianas, bisectrices, círculo circunscrito, círculo inscrita, perímetro y área.
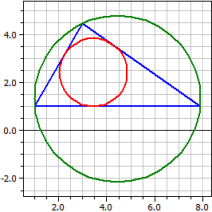
Dado: a=6, b=4 y α=60°
Vértices: A(1|1) B(7,899|1) C(3|4,4641)
Lados: 6 4 6,8989795
Ángulos: 60° 35,26439° 84,73561°
Alturas: 3,9831277 5,9746915 3,4641016
Medianas: 4,7747208 6,1480045 3,7551326
Bisectrices: 4,3855053 6,1166417 3,5464038
Círculo circunscr.: M(4,4495|1,3178) ru = 3,4641
Círculo inscrito: O(3,4495|2,4142) ri = 1,41421
Àrea: A = 11,9494 Perímetro: u = 16,899
Triángulos por tres puntos
A partir de las coordenadas de tres vértices, el programa calcula todos los elementos externos e internos (ver triángulos de tres elementos).
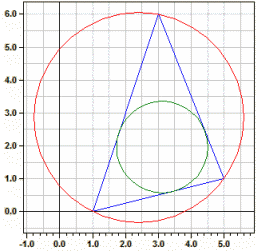
Vértices: A(1|0) B(5|2) C(5|5)
Lados: 3 6,4031242 4,472136
Ángulos: 24,775141° 116,56505° 38,659808°
Alturas: 4 1,8740851 2,6832816
Medianas: 5,3150729 2,0615528 4,472136
Bisectrices: 5,1435958 1,8879268 3,8554224
Círculo circunscr.: M(1,75|3,5) ru = 3,57946
Círculo inscrito: O(4,1352|2,5345) ri = 0,864849
Àrea: A = 6 Perímetro: u = 13,8753
Líneas especiales en el triángulo
(Nuevo en la versión 9.0)
El programa determina las ecuaciones de las mediatrices, de las medianas, de las bisectrices y de las alturas de un triángulo.
Además, los centros y radios del círculo circunscrito, del círculo inscrito y de los tres círculos tangenciales.
Dado
¯¯¯¯¯
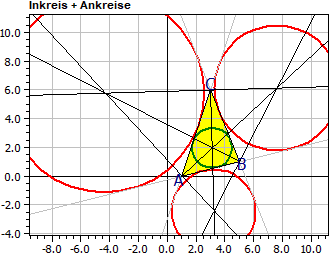
Vértices: A(1|0) B(5|1) C(3|6)
Resultados
¯¯¯¯¯¯¯¯¯
Lados: a : 5·x + 2·y = 27
b : 3·x - y = 3
c : x − 4·y = 1
Círculo inscrito: Mi(3,119|1,962) ri = 1,390
Círculos tangenciales: Ma(7,626|6,136) ra = 4,346
Mb(-4,356|5,784) rb = 6,910
Mc(3,248|-2,427) rc = 2,900
Polígonos regulares
Teniendo en cuenta uno de los siguientes elementos de un polígono con n vértices, los otros se calculan.
El lado, el radio del círculo circunscrita, el radio del círculo inscrita, el perímetro o el área.
Dado
¯¯¯¯¯
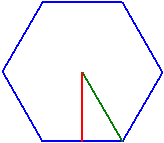
Los vértices n = 6
Perímetro p = 8
Resultados
¯¯¯¯¯¯¯¯¯
Lado a = 1,3333333
Círculo circunscr. rc = 1,3333333
Círculo inscrita ri = 1,1547005
Área A = 4,6188022
Ángulos α = 120°
Polígonos arbitrarios (Nuevo en la versión 9.0 desde noviembre 2022)
Ahora también se calculan los lados y Ángulos del polígono y se comprueba si el polígono es convexo, cóncavo o superpuesto. AdemÁs, los polígonos convexos se comprueban si tienen un incircunferencia y/o circuncircunferencia.
Vértices: Área A = 16
A(1|2)
B(4,5|0,5) Perímetro p = 15,54498
C(6|4)
D(4,5|5,5) Centroide de vértices:
E(1|4) CV(3,4|3,2)
Centroide del Área:
CA(3,46875|3,07813)
Lados: Ángulos:
|AB| = 3,8078866 ∡BAE = 113,19859°
|BC| = 3,8078866 ∡CBA = 90°
|CD| = 2,1213203 ∡DCB = 111,80141°
|DE| = 3,8078866 ∡EDC = 111,80141°
|EA| = 2 ∡AED = 113,19859°
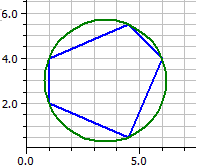
Póligono ciclico
Círculo circunscrito: M(3,5|3) r=2,6925824
Póligono ciclico:
Mapeos de polígonos
(Revisado en la versión 9.0)
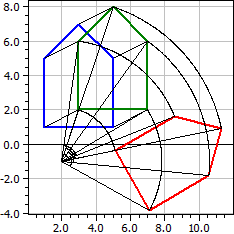
Un polígono se puede asignar de una traducción, la simetría axial, simetría punto, la rotación, homotéticas estiramiento, la transformación de corte o cualquier combinación de ellos.
Polígono original A(1|1), B(5|1), C(5|5), D(3|7), E(1|5) 1. Desplazamiento: dx=2, dy=1 ☑ A1(3|2), B1(7|2), C1(7|6), D1(5|8), E1(3|6) 2. Rotación: Z(2|-1), α=-60° ☑ A2(5,0981|-0,36603), B2(7,0981|-3,8301), C2(10,562|-1,8301), D2(11,294|0,90192), E2(8,5622|1,634)
Secciones de Círculos
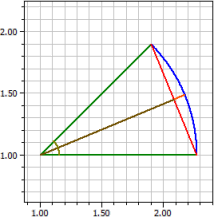
Teniendo en cuenta dos elementos de una sección circular, radio, ángulo, arco, cuerda, sección, segmento, área, perímetro, distancia entre los acordes y la altura del arco y la flecha se calculan
Dado
¯¯¯¯¯
Arco b = 1
Ángulo α = 45°
Resultados
¯¯¯¯¯¯¯¯¯
Radio r = 1,2732395
Acordes s = 0,97449536
Sección A1 = 0,63661977
La distancia d = 1,17632
Flecha altura h = 0,096919589
Segmento A2 = 0,063460604
Área A = 5,0929582
Perímetro u = 8
Tangentes a círculos (Nuevo en la versión 9.0 de febrero de 2021)
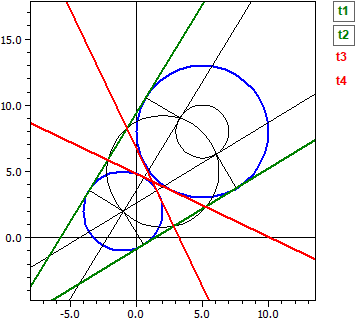
Se calculan las siguientes líneas tangentes
- La tangente a un círculo k en un punto P
- Las tangentes a un círculo k a través de un punto P fuera del círculo
- Las tangentes a un círculo k paralelas a una línea recta g
- Las tangentes a dos círculos k1 y k2
Dado: ¯¯¯¯¯ k1 : M(5|8) , r =5 k2 : M(-1|2) , r =3 Tangentes exteriores ¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯ t1: -4,2923·x + 7,04104·y = -6,36427 t2: -7,04104·x + 4,29230·y = 40,3643 tangentes interiores ¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯ t3: 1,21895·x + 2,55228·y = 12,3709 t4: -2,55228·x − 1,21895·y = -8,3709
Intersecciones en el plano
Las intersecciones entre dos líneas, una línea y un círculo y entre los dos círculos se calculan.
Dos rectas
g : x + y = 0 h : x - y = 5 Punto de intersección de g y h : S(2,5|-2,5) Ángulo de intersección de g y h: 90° Las distancias desde el origen : d(g,O) = 0 d(h,O) = 3,5355339
Recta y círculo
k : M(5|0) r = 5 g : x + y = 0 Puntos de intersección : S1(5|-5) S2(0|0)
Dos círculos
k1 : M1(5|5) r1 = 5 k2 : M2(0|0) r2 = 5 Puntos de intersección : S1(5|0) S2(0|5) Conexión de la recta : x + y = 5
